Fitting the experiment to a model is a general procedure that goes well outside the world of NMR. In our little world it is commonly called "deconvolution". Is it the same outside? While this is a word with a gentle sound, and I like using single words instead of long expressions, I think that the name is not appropriate, also because deconvolution has its own meaning and math expression. When you add a line broadening factor to a noisy 13-C spectrum, you are actually convoluting the existing peaks with a Lorentzian shape. If the line broadening factor is negative, you perform, de facto, a deconvolution. My readers are able to find all the good reasons to explain why we call deconvolution what should be actually called line-fitting and weighting what should be called (de-)convolution, and I don't argue. I also dislike the sound of the word "fit". In the following I will freely use both terms. You know what I mean.
This is one of the funniest things in NMR processing, for two reasons: first, it frees the spectrum from noise; second, it is not trivial, therefore achieving a good fit is always a cause of joy and satisfaction. In practice it only lasts a few seconds and the victory is almost certain; it's a video-game with a little less fun and much less stress. I am aware that deconvolution can be performed by the computer in an unattended way, yet I tend to believe that success requires strategy, experience, tactic, patience, luck, self-esteem and ingenuity (all in minimal doses).
The computer measures the goodness of the fit by the residual quadratic error; the user relies both on this value and on the similarity of the two plots (the spectrum and the model). There is nothing sacred in neither measure. They are only two details and I look to the whole picture. The numbers you get by line-fitting are always to be compared to other numbers. For example, you want to compare the concentrations of a metabolite in different samples. You can judge by yourself if the variations make sense, but you can also compare your concentrations with the literature values, or the values found by another analytical technique, or the values found fitting a different peak of the same molecule, etc...
There is the statistic-kind of analysis, the so-called error analysis. I agree that some games can be boring, but statistic is way too dull! (The dullest discipline I have ever come in contact with). If it only yielded meaningful numbers, I would happily tolerate it. When I have found or calculated those confidence ranges, I have seldom found them worthy of any confidence. Probably the theory of error analysis doesn't apply to NMR (the single points aren't independent observations, the errors aren't distributed normally, etc...) or, more simply, I couldn't find anybody willing to teach applied statistic to me.
I am going disclose my secret strategies tomorrow. Before closing the post, I want to pass the concept that deconvolution is not a better method than integration in all circumstances. While accurate integration already has its requirement (complete relaxation between scans, flat baseline), deconvolution also requires good magnetic homogeneity, and elevate digitization. Integration is affected by noise in a limited way (and when the noise is much higher than the signal there's no method that works). The advantages of deconvolution are that you can measure the ares of overlapping peaks, but also the frequencies and the linewidths.
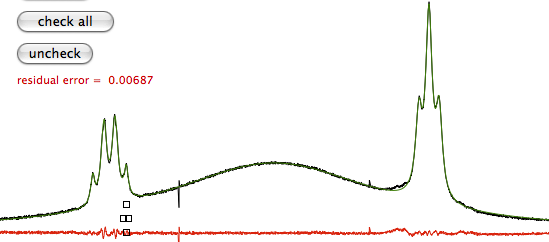picture taken from www.inmr.net
No comments:
Post a Comment