Thank You

There are other topics to write about, as promised at the beginning of this series.
Being that keeping a blog takes time and soon becomes a boring activity, I have decided to give you links instead of new pages. All the articles in the list below have been written by myself over the last couple of years. I could reorganize them into a more organic and readable form, but the concepts are already clear enough.

• Manual Corrections
• Automatic Baseline Correction
• Automatic Integration
• Perfect-Looking Integrals
• Visual Weighting
• 2D Phase Correction
• Further Hints for 2D Phase Correction
• 1D Phase Correction
• Automatic Phase Correction
• Non Linear Methods

I'll continue the blog when I find something new to say. I thank you all that have been reading me daily during the last month. Yesterday the blog received 84 visits, which was the July record.

Torrents of Cracked NMR-Warez

My most popular post, in two years of activity, has been the infamous "TopSpin NMR Free Download". That single (short) post has received as many comments as the rest of blog (sob!). People were so prompt to fix their anger in words but nobody was touched by the idea of starting a discussion. Unless you call discussion an exchange of flames. I have learned the lesson, in my own way. This time I have chosen a more explicit title, so nobody can say he arrived here with pure and saint intentions.
I myself haven't changed my mind. Year after year, a lot of money is spent to acquire/upgrade NMR instrumentation and software. Attending a conference is not cheap and renting a booth there is really expensive. The number of computers sold keeps increasing year after year. How is it possible that there is so much money in circulation and, at the same time, people cry because they can't pay an NMR program (but could nonetheless find the money to buy a new computer...) ?
Our society spends a lot of money to buy goods that are never used, or misused, or are notoriously dangerous for the health or the environment. If you really want to buy a thing that you aren't going to use, don't buy a computer. Just think at the environmental cost of disposing of it in a few years to come. Don't buy a cell phone. Your drawer is already full of old items you don't know what to do with. Don't buy a book. Just think at how many unread books are accumulating dust in your library. Buy software in digital form. It's a wiser form to waste your money.


If you came to this blog by accident, would you please have a look here around and try reading any other post, just to develop a more correct idea of what this blog is about?
In the last 6 weeks I have been publishing an article per day, with few exceptions. My activity has had no effect on the traffic. For example, the blog was more visited in April, a month in which I wrote a single article in total.
Tomorrow I will therefore conclude the current series of daily articles.

Recipe to Remove the t₁-noise

Take a column of the processed 2D plot (column = indirect dimension). Use a mapping algorithm to identify the transparent regions (not containing peaks). In the following I'll call them the "noisy regions".
The idea is to delete these region. Setting all their points to zero would be too drastic and unrealistic. What you do, instead, is to calculate the average value in this region. More exactly, the average of the absolute values. At the end you have a positive number which is a measure of the noise along that column. Repeat for all the columns. At the end you have the values of noise for each column. Noise is higher when there is a big peak (on the diagonal or elsewhere). Noise is low where there's no signal. Annotate the minimum value for this noise, let's call it "min". Now, pick again each column. Divide its "noisy regions" by the value of their own noise, then multiply them by "min". The portions containing true peaks are not affected.
The result is that now all the columns show as much noise as the least noisy column. In other words, the noise is = min everywhere.
The merit of this technique is that the final spectrum looks extremely natural, even if it's not. You can't cancel a peak by accident, because nothing has been zeroed.
De-noising, as describe here, can be successfully combined with baseplane correction and symmetrization. Remember that baseplane correction comes first and symmetrization always come last.

Second Love

Since the beginning of this series of "lessons", the stress has been on 1-D processing. I have shown that 1-D processing can be as tricky and important as 2-D processing. If you are working exclusively with large bio-molecules you may well live with the sensation that there's no NMR with less than 2 dimensions. The NMR field is divided in many rooms and there's not enough communication among them. I have attended several NMR conferences where there was indeed the possibility for the groups, working in distant field, to merge their knowledge for a week. My impression is that every one keeps speaking his own language and keeps doing the same things for decades. NMR is not a unifying technique. The main link between the researcher is not their society, but the factory that builds the instruments.
Today I want to write about a couple of processing operations that are specific to 2D. Symmetry is the first example that comes to my mind. In homo-nuclear correlation spectroscopy, we expect that the two halves of the map, divided by the main diagonal, are the mirror image of each other. They aren't for a couple of reasons:

• The line-widths along the indirect dimension are generally larger.
• The t₁ noise is specific to t₁, as the name says.

The software can force the two halves to be the same. Every couple of corresponding points is compared. The point with the lowest absolute value is the "correct" point; the point with the highest absolute value is replaced. In the case of J-resolved spectra, the axis of symmetry is different, but the principle the same.
After the substitution, the resulting shape of the peaks is that of a pilaster, instead of a column. I prefer the original shape, but in many cases the advantages are overwhelming. My rule is easily stated: I symmetrize all my COSY. Both the COSY experiment and symmetrization looks terribly old and out of fashion, but they are so simple and fast (I mean: the gradient enhanced variant), that I always acquire a COSY, if I must acquire another 2D of the same sample. The COSY comes almost for free. They say that symmetrization might create false cross-peaks. This is right, yet it's a rare event and not a dangerous one. If you have some experience you can usually recognize the false cross-peaks. If you haven't, you can compare the symmetrized and unsymmetrized versions of your COSY. It takes a few seconds.
I don't symmetrize my phase-sensitive spectra, unless the noise is exceptionally intense. In the phase-sensitive case I feel that the original shape of the peaks carries precious information (like a fingerprint), and that a baseplane correction is enough to clean the spectrum. You can combine baseplane correction and symmetrization, only in this order. Another trick, which Carlos taught me, can remove the "t₁ noise". Actually it's a modification of the baseplane correction and it's more an aesthetic trick than an operation to clean the spectrum. Tomorrow I'll describe my personal implementation of it.

Report Generator

The natural complement to the Multiplet Analyzer is a Report Generator. The former starts from the list of frequencies (the output of peak-picking) and generates a table of chemical shifts and couplings. The Report Generator starts from this table and generates a formatted list, ready to be inserted into a patent or an article; the format is compliant with the rules dictated by the patent office or by the receiving journal, etc..
It's counter-productive, for a software vendor, to explain all this details and intermediate stages. It's more impressive to state that a program can start from the FID and automatically generate the article (and maybe even sending it via email to the editor of the JOC!). If such a monolithic thing really exists, it would be a case of bad design, but the marketing appeal can't be argued.
Selling a program is easy. Convincing the customer to use it, that's difficult!

We have seen that the multiplet analyzer is limited to first-order signals. We have also examined other wonderful weapons at our disposal: the simulation of spin systems, to extract the NMR parameters from second-order multiplets, and deconvolution, to untangle overlapped signals.
A software vendor can't say: "Our research team is working hard to deploy a New Integrated Software Solution (TM) that automatically solves the most difficult cases" and in the meanwhile leave the user alone. The customer needs to publish his article right now, he can't wait for the next release of the software.
We have 3 established, long-standing and effective methods. They can be applied to different regions of the same spectrum. Let the Report Generator act as a central server, capable of accepting input by any method, even those that I am forgetting now, and of sending out the results in many different formats.

Suggested Reading:
The J Manager as a Center of Gravity.
This tutorial can be followed in practice, because it includes the same sample files that are shown into the pictures. There are also step-by-step instructions. The concept should be clear.

Multiplet Analyzer

Not all the spectra are second order. Actually, today's marketing insists to generalize that, in our new century, almost all the spectra are first order. Such a generalization makes sense if you process a spectrum (or less) per year, otherwise your destiny is to meet, sooner than you expect, something second-order. It's true that you are allowed to describe your spectrum as a sequence of generic multiplets, avoiding a more detailed analysis. This is tolerated but hasn't become the recommended practice yet. That said, there are certainly a lot of first-order multiplets in our spectra and extracting shifts and J it's an easy but tedious task. Can the computer help us? See for example the following spectrum of 1-pentyne in CDCl₃.

(The peak at 1.56δ is an impurity). There are, from left to right, a triplet of doublets, a triplet, a sextet and another triplet. The manual extraction of parameters is easy. Let's start from the sextet, because it's a curious rarity. It's enough to know the frequencies of the two external lines. The distance, divided by 5, gives the J. The sum, halved, gives the chemical shift. If you use a pocket calculator, there is the risk of a wrong transcription of the values from the monitor to the calculator and from the calculator back to the computer (for example into MS Word). The risk is low, but not zero. Besides this risk, the whole operation is time-consuming. Finally, it's not cool: you have to move cyclically from the NMR software to the pocket calculator to MS Word, etc...
Being it a simple operation, it can be performed automatically by the computer. It will not start directly from the data points, but from the same values used by an operator: the list of frequencies (peak-picking), the intensities at these frequencies, the list of integrals. These lists can also be generated automatically; in conclusion the whole process can be performed in automatic fashion. In practice, however, it's not convenient. Why? Suppose that the maker of the program claims that the automatic method works in the 99.9% of the cases. That's a generous claim, difficult to trust. For example, if the program doesn't recognize our impurity at 1.56δ as such (see picture above), it will fail to recognize the multiplet as a sextet. But, even if we believe the claim, how do we know if our spectrum belongs to the 99.9% or to the 0.1% of failures? We are forced to check the output with care. The time saved with the automatic processing will be lost for the check.
In my opinion, it's best to perform the integration and the peak-picking first (manually or automatically) and perform the check at this stage: the inspection is visual, not textual, therefore faster. In the case shown by the picture, this is the moment to remove the entry "1.56" from the list of frequencies. When all is ready, proceed with the computer-assisted extraction of the NMR parameters. A picture is more explanatory. Refer to your software or give a glimpse to this tutorial.
Although not a rule, Multiplet Analyzers ignore and remove the roof effect. Take for example our sextet. It can be recognized as such only if the intensity ratio is 1:5:10:10:5:1. The leftmost multiplet also has 6 lines, but the intensity ratio is 1:1:2:2:1:1, therefore it's recognized as a triplet of doublets. The roof effect prevents the recognition, therefore it's removed by averaging (symmetrization). For example, if the ratio of a triplet is 0.9:2:1.1, the computer calculates the average of the outer lines and the result is the theoretical 1:2:1. There's a notable exception. When there are two lines only, a single solution is possible, the doublet. When the lines are three, if we assume that all nuclei have spin = 1/2, the solution is still unique.
The roof effect can also exploited, in these cases at least. Like the old textbooks say, the chemical shift of a doublet doesn't correspond to the middle frequency, but to the center of mass. This is the single case I know when a multiplet analyzer performs a second-order analysis. I don't know if the center-of-mass rule is general and if all today's program observe it.
There's another, more obvious, rule to follow: any two coupling partners must show an identical splitting. In practice, the values extracted from two multiplets are rarely identical. Only the user can decide what to do. She can either:

1. Substitute the original values with an average value.
2. Remove what appears to be the less accurate value and put in its place the splitting shown by the partner.

Turning Point

The turning point in dynamic NMR was the article "DNMR: the program" by Gerhard Binsch (JACS, March 12, 1969). The article said: if we monitor chemical exchange by the coalescence of two singlets, a large variation of the rate is reflected into a small change of the spectrum. Therefore our estimate will be inaccurate.



If, keeping A and B as they are, we simply add a third nucleus C, coupled with both A and B, see what happens:



Now a small variation in the rate of exchange is the cause of a large change in the spectrum. Therefore we can estimate the rate (by simulation) with higher accuracy and confidence.
40 years later the lesson has not been learned yet and there's people who prefer to add a methyl group to their compounds to monitor the exchange rate by the coalescence of the singlets. I can understand this choice if the reason is to maximize the intensity of the signals.
I suspect, however, that the true reason is a different one. There is an approximate formula from which you can calculate the rate of exchange from the temperature of coalescence.
It's very approximate, but much easier to put in practice. A single spectrum and a simple formula instead of collecting 10 spectra and fitting each element of the series, then plotting the data to extrapolate the Eyring equation... The accurate method not only is much faster, it also avoids using a computer. The problem, today, is never the computer but always the software. Is the 40 years old DNMR difficult to obtain? You don't need DNMR: today you have WinDNMR, Spinworks, Mexico, iNMR....

Hot and Cool

Dynamic NMR includes chemical exchange and internal rotations. They are the same thing, observed via NMR. If the rate of exchange is low, you can start from a non-equilibrium situation and measure the changes of concentration over a period of hours or days. When the rate is higher, you study the situation at equilibrium, either by saturation transfer or by line-shape analysis. The latter is akin to the simulation of spin systems seen so far. There is one more parameter, the exchange rate constant (assumed to be first-order). If you have an exchange among many sites, you can have several different rates, but it's rare.
The visible effect of chemical exchange is the broadening of the lines. The effect is dramatic at the coalescence, when two of the corresponding signals of the exchanging species become one.
The temperature of coalescence depends on:

1. the exchange rate
2. the difference in Hz

The direct consequence is that:

1. a species with n signals can have up to n different temperatures of coalescence (in the pictures, n = 3)
2. they change with the magnetic field

Look at the coalescence peak marked as CC. How can you extract two values of chemical shifts, 2 Js and one rate of exchange from that mountain? Well, you can't start from here. You start from the spectrum at a low temperature, where there's no exchange, and measure all the parameters but the exchange rate. Then, hopefully, it would be enough to introduce this rate to simulate the spectra at all the other temperatures. In practice, everything always changes, but slowly. At the slowest temperatures and at the highest ones, it is difficult to separate the effect of relaxation from that of exchange, because both contribute to a similar broadening. Near coalescence, the effect of the broadening caused by exchange is two orders of magnitude larger than the broadening caused by relaxation. In practice, even if the error in estimating relaxation is 100% of the value, the error in estimating exchange is only 1%, therefore more than acceptable. Far from coalescence, instead, you have to be cautious. The simplest thing to do is to verify that the T₂ changes monotonically with temperature.
In practice you collect 10 or more spectra at different temperatures. You also need the calibration curve of your probe (the instrument only reports the temperature around the probe; you need to know the temperature inside it, which can be measured spectroscopically, with a sample of methanol).
After extracting, by simulation, the rate of the exchange at each temperature, the plot of ln(k/T) versus 1/T gives a straight line; the enthalpy of activation can be derived from the slope and the entropy is derived from the intercept (Eyring equation). It's a mystery if these enthaply and entropy quantities remain the same at all temperatures or not. The linear plot should tell these things and will also tell if the whole work was correct or not.
If your software allows a computational least-square fit you can well try it, but I personally prefer the simple, old-style, manual fit. In theory there's no advantage in using a computational method, because the algorithm that finds the global minimum hasn't been invented yet. There is, however, something that a computer can do and we can't. It is the grand single fit of the whole experiment (the 10+ spectra) to find, via least squares, not the rates of exchange but directly the enthaply and entropy of activation. (They told me) the existence of this program has been mentioned in literature (years ago) but the program itself is not available.

Relationships

A system of 3 different protons has 12 lines. The same system, made of ²H nuclei, has 27 lines. Both systems can be described with 3 shifts and 3 coupling constants. That's obvious. Add a common line-width: 7 parameters to describe 27 or 12 lines.
There are many other "obvious" relationships that often reduce the degree of freedom of the problem. The group CH₃-CH-CH₃ contains many more hydrogens, but is described by only 2 or 3 parameters (because of the magnetic equivalence). A para- (or ortho-) di-substituted benzene, if the substituent is the same, is symmetric: all parameters are duplicated. Tin is a mixture of isotopes, 3 of them are magnetically active. If you want to simulate the proton spectrum of a tin compound, you have to declare 3 or 4 systems, but their parameters (shifts, couplings), neglecting the isotope effects, are the same. The above 3 examples can be handled by the software. Summarizing:

1. magnetic equivalence
2. symmetry
3. isotopic mixture

The gain in computationally speed that derives from this awareness is not important. The real advantage is the simplified book-keeping. Compare, for example, this definition of ODCB:
with the symmetry-aware equivalent:
(pictures courtesy of www.inmr.net)

While it's important that the software directly implements the listed concepts, it's also useful that it understands additional relations defined directly by the user and specific for his/her problem. The first picture exemplifies the idea. The user renounced to the advantage of symmetry and the table of couplings is large. The number of parameters is still low, because he declared 4 relationships. For example, he declared that the shift of hydrogen C is the same as hydrogen B. This is the simplest form of relation (equality), that is implemented through symbolic parameters.
When are relations really useful? First example: transverse relaxation times. Quite often these simulation are performed assuming that all the nuclei have the same T₂ (same line-width). In a few cases, when one or two nuclei relax faster, you are forced to declare the individual widths. To keep the total number of parameters low, I prefer an intermediate solution: dividing the nuclei in two classes. There are only two parameters for the line-widths. This is possible if the software allows me to declare symbolic values. Excel allows me to fill a cell with numbers, text or expressions, at will, but doesn't understand NMR. I have cited Excel just to make the concept clear. The above picture shows that is possible to use symbols instead of numbers inside an NMR software.
Exploring the same web site you can see that symbolic values have been able to solve all sorts of problems:

• dipolar couplings
• isotopic mixture and chemical exchange

Checklist

Now that you know about the three main approaches, where to go from here?
If you want to use one of the methods for fitting a spin system (see yesterday's post), the simplest (and single) thing to do is to read the manual of your program. If it's too short, reading it will require a little investment of time. If it doesn't help, it either means that your program is extremely intuitive or that you need a different program. If, instead, the manual is very long, there are two cases: either the program is very powerful and well documented, so there's a lot of things to learn from it, or the program and its manual are a crappy mess.
There are a lot of advantages if the same program performs both processing and simulation; it means: less things to learn, a couple of export/import operations are avoided, there are more users (i.e. the program has been more tested), the interface is probably simplified (because they are general-purpose programs targeted at the casual user). The disadvantages (compared to a specialized program) may be a limited set of features.
It's also extremely convenient if the same program implements all the three fitting methods outlined yesterday AND dynamic NMR. This gives you the option to switch with no effort from any method to any other. If, instead, you use a different program for each method, and the first method you try turns out to be inappropriate, you have to redeclare the terms of your problem and re-import the experimental data... quite boring!

Comparing different programs
Not all programs are equal. Features to look for when comparing two of them:

1. Can you adjust the parameters manually (graphically)?


2. Are the plots (experimental and theoretical) overlapped?


3. Can you define symmetry relations?


4. How many systems can you define?


5. Can you define relations between parameters of different systems?


6. How many nuclei can you define?


7. Can you define all kinds of spins?


8. Are dipolar couplings handled?


9. Is Dynamic NMR included?


10. Is Total-Lineshape Fitting included?


11. Is a LAOCOON-like Fitting included?


12. Can you change the shape of the peaks or are they exclusively Lorentzian?


13. Are the chemical shifts measured in ppm rather than in Hz?


14. Can you declare a spin system by its ChemDraw formula?


15. Once you have extracted the parameters, can you generate formatted lists of these parameters? How many formats?


16. If your program includes a "multiplet analyzer", does it talk with the simulation module?

Arsenal

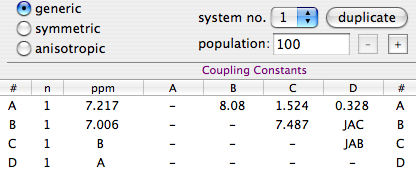
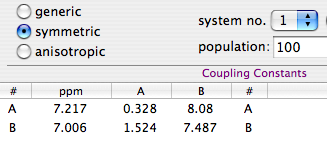
When you are able to process an NMR spectrum; when you are also able to simulate the same spectrum (starting from the definition of a spin system); then you are ready to fit the two, one against the other. People tend to skip all the intermediate stages. I would not. If I can't write the single words, I won't be able to write a sentence. Yesterday I said that the simulation of a spin system is a useful exercise to understand a few principles of NMR; now I need to stress that it's also a useful exercise before you move on to the extraction of the NMR parameters by simulation. Once you have the two main ingredients, the experimental spectrum and the synthetic one, there are three main methods to perform the fit; each one has a reason to exist.

(1) Manual Adjustment
This can work if the spectrum, or portions of it, can be interpreted with first-order rules. Chemical shifts are easy to fit manually, because it's enough to literally drag each multiplet in place. The coupling constants can be adjusted in order, from the most evident (large) one to the most difficult (small) to extract. The process is simplified when the experimental multiplets are well resolved; in other words: apply a Lorentz-to-Gauss resolution enhancement by weighting the FID. Manual adjustment has become quite popular after the advent of interactive applications in the 90s. Don't dismiss it as "naive": it is certainly more accurate than extracting the coupling constants directly from the list of frequencies (which is an accepted and widespread practice). Visual fitting can be difficult with second-order spectra, but not for a skilled operator. The trick of the experts is to monitor the position of the weak combination lines. They are forbidden transitions that appear as tiny satellites. If you can simulate them exactly, the rest comes naturally in place. They are diagnostic, like canaries in a coal mine.

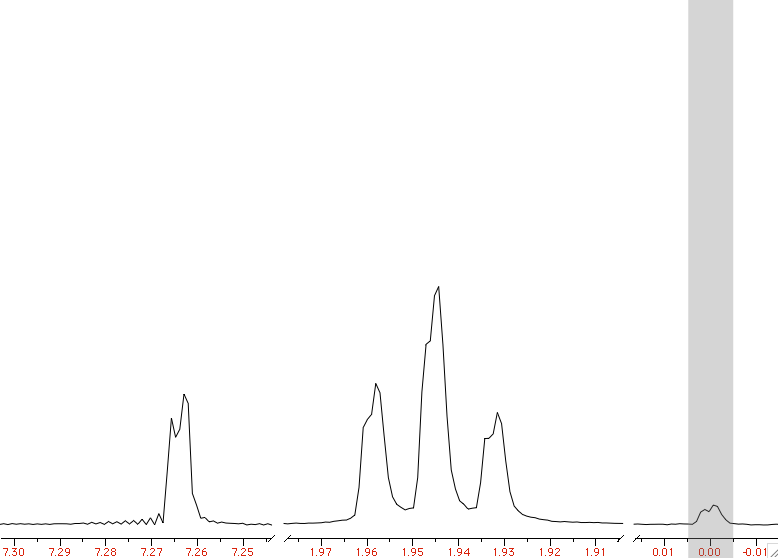
(2) Laocoon
This was the name of the first popular program used to extract the Js from second-order, complicated multiplets. The program is no more in use today, but the method is still excellent. Quite simply it compares a list of experimental frequencies with a list of theoretical lines. Then improves the spectroscopic parameters according to the least squares principle. A lot of useful information is ignored, but this is also the strength of the method. When there is too much noise, or the baseline is problematic, or a solvent hides part of the spectrum, etc... you simply can't extract all the information from the spectrum, or you can but the intensities are not dependable. It's better to feed the algorithm with minimal selected data of high quality than hoping that a mass of errors can mutually compensate each other. With Laocoon it's not even necessary to match all the lines; as you can expect, the condition is that the number of parameters to guess must be less than the number of the lines. Despite the simplicity, this method requires more work, because you have to assign/match each experimental line to a theoretical line. This job looks trivial at the end of the process, because it's enough to match the lines in order of frequency. It's different when the starting guess is largely inaccurate. A single mismatch, in this case, is simple to discover, if you know the trick. The column of the residual errors will contain two large and opposite values. They correspond to the "swapped" lines. All considered, the most difficult part, for the user, is to read the manual of his/her program.
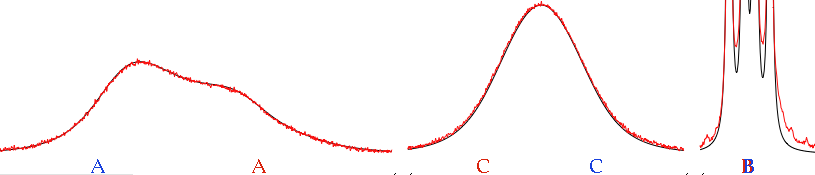
Here, more than in any other case, a Lorentz-to-Gauss weighting is beneficial: remember that you are not starting from the raw data points, but from the table of frequencies ("peak-picking"). It is well known that the position of the maxima of a doublet doesn't coincide with the true line frequencies, when peaks are broad.

picture courtesy of the nmr-analysis blog.

(3) Total Line-shape (TLS)
I suspect that this approach derives, historically, from dynamic NMR, (the simulation of internal rotations, like in the case of DMF). You can, indeed, simulate a "static" system with a dynamic program, if the exchange rate is zero. DNMR (and the programs that follow the same principle) don't recalculate the single lines (frequencies, intensities) but other sets of parameters that are used, eventually, to create the synthetic spectrum (plot). The latter can be compared, point by point, to the experiment, and the least squares are calculated from the difference. This is a great simplification for the user, compared to LAOCOON, because it's no more necessary to assign the lines. An higher quality of the experimental spectrum is however required, because the program now also employs the intensity information, and this information must be correct. Therefore the baseline must be flat and no extraneous peak can be present (it is trivial, however, to artificially delete isolated extraneous peaks/humps). Summarizing: you must spend time on processing the experimental spectrum.
We have seen that the first two methods prefer gaussian line-shapes.
This is not necessary with TLS, but we have the inverse problem: if you have already prepared the experimental spectrum for the other kinds of fit (with Gaussian shapes), can you perform a total lineshape fit? The answer is "NO" if we look at the original formulation of the method, but in practice it is possible, with some commercial package, to work with both kinds of shapes (and anything in between too).
Don't be mislead by the name "Total": nobody fits the whole spectrum, but only portions of it. Most of the tricks we learned when fitting singlets (and collection of not-organized peaks) can be recycled with TLS. Actually, there is a minimal difference, from a mathematical point of view. In TLS, the algorithm varies a collection of parameters. They give a collection of lines, that are used to simulate the spectrum. In deconvolution, the algorithm directly start from the frequencies. That's the first difference. There is also a procedural difference: TLS has a built-in mechanism to escape from local minima. In practice, in the first stage of the fitting, a line broadening is applied that blurs the details. Once the multiplets has been set in the proper place, the broadening is removed and the details are taken into account. With plain line-fitting, there is no such need, because the first guess is extracted from the experimental spectrum itself, therefore everything is always in the right place (nearly).
If we called the previous method by the name of the first program implementing it, then TLS could be called, in a similar way, "DAVINS".

Spin Systems

A fortnight ago we saw how to fit a spectrum with a collection of curves. A more evolute approach is to fit the spectrum with a collection of NMR parameters (shifts and Js in the first place). There are two reasons to prefer the latter approach:

1. you introduce logical restrictions into the model, for example you specify that the components of a triplet are in the ratio 1:2:1
2. you overcome the job of measuring shifts and Js from line positions

Simple line fitting to a generic collection of lines remains the best choice for singlets, simple multiplets and when you are not interested at all into the frequencies, but only into the intensities. Simplifying, curve-fitting (the so-called "deconvolution") is more about areas, spin system analysis is more about energies.
We have arrived to a large topic from an unusual path. We are in the field of quantum mechanic. It's easy in theory and, in practice, when the nuclei are few. When the number of nuclei in a spin system grows, no computer is fast enough to calculate precisely what happens. Somebody has also proposed to invert the roles, and create a super-computer with a large enough spin system (the quantum computer). That's even more difficult (try building a real molecule with 20 different nuclides!). When the number of nuclei is limited (e.g.: 10 protons), there is however no problem, at least with the older programs that diagonalize the Hamiltonian. I dedicated a post to the modern programs that can follow the evolution of a system under all kinds of effects. They have more calculations to do, are limited to smaller systems and, as it appeared from my old post, are oriented towards solid-state NMR.
Older programs are more popular in liquid-state NMR. I have already cited the free gNMR and SpiWorks. I have probably never cited Perch LE and Wind-NMR. Thay are all free (for academic users at least) and they all require Windows. Can you suggest a free solution for Linux and Mac users?
It's not a surprise that, which such an abundance of free solutions, the commercial applications, in this present moment, are ignoring the field. The race now is at predicting the spectrum directly from the chemical structure. That's the third level. At the first level we have the frequencies and intensities of the single lines. At the second level we have shifts and couplings. At the third level we have the structure. If you only have the third level, you can verify your spectrum against the prediction, but if you want to publish your data you need to extract the Js directly from the experimental data. You can't do that without the second level, unless you are glad to standardize all your reports into lists of unspecified multiplets, like:
7.24, m (2H); 4.14, m (2H), 2.36, m (8H).....
The simulation of spin systems is also becoming a popular exercise for chemistry students new to the world of NMR. It's amazing how fast the magnetic field can change, even by orders of magnitude. After a while the game becomes repetitive, but it remains highly instructive for newcomers. An excellent starting point is an article by Carlos on the NMR Analysis Blog. It should be, however, complemented by practice, more than by further references. There is a minimal library of ready examples for Mac users. It contains the classic cases (orto-di-chloro-benzene, DMF), plus templates for small and medium-sized systems of 1/2 nuclei. In the case of DMF you can change not only the magnetic field, but also the temperature.
I don't want to bother you with theory, but one thing at least must be said: geminal couplings usually have a negative constant!
One more thing on practice too: Carlos said that not all NMR signals are symmetric. Personally I still believe into the myth that they are symmetric, like the human body. To be precise, neither are symmetric, but in practice this precision is useless and misleading. I rely on the IDEA of symmetry to recognize a friendly face and I rely on the IDEA of symmetry to recognize NMR signals. By the way: they too are friendly!

Fixed Focus

All cameras need to be focused before shooting. There are 3 alternatives: manual focus, autofocus and fixed focus. The latter is an economical choice that can't work under all circumstances, it's OK only when the depth of field is large enough. This depth depends on the characteristics of the lens.
I can see a similarity in NMR spectroscopy. The phase correction of an high-resolution spectrum is like a lens with a limited depth of field (think to a telescope, if you are more familiar with them; the telescope is an example of a lens with a narrow depth of field). Starting from the optimal correction, a minimal change in the phase correction parameter (movement of the lens, in the parallel example) causes a visible negative effect on the spectrum (clearness of the image). It's not enough to copy the phase correction from a spectrum to the other, you must use either manual or automatic correction or both. Like it or not, you'll become an expert in the field.
Weighting is much more tolerant to a small change of the parameters, to the point that most of us use the "Fixed Focus" approach. We can even store the optimal value inside our standard parameters and forget about it. When you have forgotten it, it's arduous to improve your skill; DSP (digital signal processing) contains too much theory and practice is time consuming.
My rules are:

1. Weighting is an alteration of the spectrum. An altered spectrum may look ugly, don't worry.
2. It's more important to know what I want to obtain (where I want to go) that the way to go there, because many roads lead to the same place, but I must be able to recognize my destination if I arrive there.

While I usually recommend to observe and practice, because 50% of NMR can be deducted with common sense, there is a case where you need the theory, otherwise you go nowhere. If you keep weighting a standard COSY spectrum with the same functions that you use in 1D spectroscopy, you'll always get star-shaped peaks like this:
[after exponential weighting along both dimensions]

It's only theory that tells you that a symmetric FID corresponds to a symmetric spectrum, therefore if your weighted FID has a symmetric envelope, the dispersion component will be attenuated in frequency domain. In simpler words: use a sine-bell. It's counter-intuitive to zero the less noisy part of your spectrum, but look at the final effect:
[after weighting with two pure sine bells]

Recollection

Before the touristic digression, we were slowly coming back to an old topic: Reference Deconvolution. If you are new to this blog, RD it's an alternative technique to weighting. Think at it as "tailored resolution enhancement" or "shimming-after-the-fact". I commented on it in two recent articles:

Reference Deconvolution in Theory

Reference Deconvolution in Practice

Tremiti Islands

Last Thursday I visited these islands for the first time.



Pictures by Maria Luisa.

Asterisk or pizza?

At the basis of weighting there's the convolution theorem.
FT( f ⋅ g ) ∝ FT(f) * FT(g)
which can also be written as:
FT( f ⋅ g ) ∝ FT(f) ⊗ FT(g)
The choice depends, exclusively, on which symbol you use to indicate the convolution operation. If, after reading the linked Wikipedia pages, you feel like being still at the point you had started from, I can propose a simplified approach, based upon Fourier Pairs and practical examples. If, in time domain, you have an exponential decay, after FT you get a Lorentzian curve. The two functions form a Fourier pair. The Gaussian function pairs with itself. A stationary sinusoid pairs with an infinitely narrow line (a nail pointing upwards). It's a curve with no shape and no width (but it has a frequency). Convolution of two curves yields a third curve with the shape of both ancestors and a patrimony (line-widths) equal to the sum of the widths of the ancestors. You can think at the result curve as an empty and opaque envelope with no shape, with both ancestor curves inside. The envelope adheres to the content, so you can see the cumulative shape.
The natural NMR peak can be described, in time domain, as the product of a stationary sinusoidal wave with an exponential decay. This dumped sinusoid forms a Fourier pair with the convolution of a nail with a Lorentzian curve. This is the convolution theorem (applied to NMR): multiplication in time domain is equivalent to convolution in frequency domain. If you consider the wave as the substrate and the exponential decay as the weighting function, the result takes the frequency from the former and the shape from the latter. That's OK. You can't do the contrary (positive substrate and oscillating weight). If your weighting function oscillates, all the peaks will show an extra splitting.
Let's give, now, some reference formulas. We'll use the symbols:
W = full linewidth at half height, always measured in Hz
ν = frequency (Hz)
ω = 2 π ν = angular frequency
The exponential decay, in time domain, is described by a single parameter λ:
f(t) = exp( - λ t ).
It forms a pair with the Lorentzian curve in frequency domain:
F(ω) = λ / (λ² + ω²).
The latter has linewidth:
W = λ / π.
That's the only parameter I consider, instead of λ, because W can be directly compared to natural signals or to the gaussian broadening.
The Gaussian curve, in time domain, has the formula:
g(t) = exp( - σ² t² / 2 ).
The other component of its Fourier pair is still a gaussian function:
G(ω) = √{ 2π } ⋅ exp[ -ω² / (2σ²) ] / σ.
σ = π W / √{ ln(2) } ≅ 3.77344 W.
The exponential lends itself to both kind of uses (it can increase either the sensitivity or the resolution, it's enough to invert the sign of λ). You can also define a new function:
1 / g(t) = exp( σ² t² / 2 ).
to increase the resolution. It's unmanageable: σ could only have near-to-zero values (otherwise the noise becomes intolerable); to the best of my knowledge, nobody has ever used this abort of weight.
We have arrived at dividing, instead of multiplying. If multiplication in time domain is equivalent to convolution in frequency domain, then division is equivalent to deconvolution...

If I Had a Bell

Weighting functions are so easy in practice and so (apparently) difficult in theory, that I wonder if we can just ignore the latter and pretend it doesn't exist. It's a matter of language. Instead of moving towards simplification, we keep creating more names, more languages, more ways to measure things. If you have learned NMR from the literature, you'll discover a different language in software, and can't find the vocabulary for the translation. The same happens when you want to write your own article: how you describe your NMR processing? It's the inverse translation. Last but not least, different softwares have different names and units for the weighting functions. Don't be mislead by the names, what matters is the shape of the window function. Ideally, it should be reproduced into your manual. Given that the shape often depends on a user-settable parameter, they can't illustrate all the possible cases. You can, however, ask the program to show the plot of your weighting function and/or the weighted FID. This is the best vocabulary. If the function grows (moving from left to right), then it can enhance the resolution.
Apart from this effect of visual translation, it's neither necessary nor advisable to observe the effect of the weighting function on the FID, when you can directly observe the effect on the spectrum in frequency domain. The FID is dominated by a few intense signals, often coming from the solvents, that are of little importance to you. In frequency domain you can monitor the effect of weighting on the important signals only.
Remember that weighting means selective attenuation, but also alteration and degradation, which you must be ready to accept: it's a part of the game. It improves the appearance of some signals and not of others. I go to the frequency domain, zoom into the region that I want to improve, and monitor the effect of varying the parameters (just like phase correction).
In some cases there's no parameter to adjust. Typical is the case of the squared cosine bell. It has a shape similar to that of a gaussian bell and it means that you could equivalent similar results using either. It's easy to calculate which value you need for the sigma, in case you choose the gaussian function, but it's even easier to use a cosine bell, with no parameter at all to set!
blue: weighted with a squared cosine bell
red: weighted with a gaussian bell (line broadening = 0.93324 / acquisition time).
The example contains four lessons:

1. non branded weighting functions can be better than the branded ones
2. anybody can be creative with them
3. there's no optimal weight and, even when it exists, a small variation corresponds to another weight that's almost as good, for all practical purposes.
4. If your software provides a limited number of functions, it doesn't mean that your possibilities are limited.