Hot and Cool

Dynamic NMR includes chemical exchange and internal rotations. They are the same thing, observed via NMR. If the rate of exchange is low, you can start from a non-equilibrium situation and measure the changes of concentration over a period of hours or days. When the rate is higher, you study the situation at equilibrium, either by saturation transfer or by line-shape analysis. The latter is akin to the simulation of spin systems seen so far. There is one more parameter, the exchange rate constant (assumed to be first-order). If you have an exchange among many sites, you can have several different rates, but it's rare.
The visible effect of chemical exchange is the broadening of the lines. The effect is dramatic at the coalescence, when two of the corresponding signals of the exchanging species become one.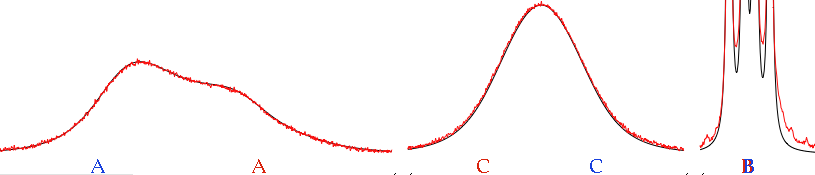
The temperature of coalescence depends on:

1. the exchange rate
2. the difference in Hz

The direct consequence is that:

1. a species with n signals can have up to n different temperatures of coalescence (in the pictures, n = 3)
2. they change with the magnetic field

Look at the coalescence peak marked as CC. How can you extract two values of chemical shifts, 2 Js and one rate of exchange from that mountain? Well, you can't start from here. You start from the spectrum at a low temperature, where there's no exchange, and measure all the parameters but the exchange rate. Then, hopefully, it would be enough to introduce this rate to simulate the spectra at all the other temperatures. In practice, everything always changes, but slowly. At the slowest temperatures and at the highest ones, it is difficult to separate the effect of relaxation from that of exchange, because both contribute to a similar broadening. Near coalescence, the effect of the broadening caused by exchange is two orders of magnitude larger than the broadening caused by relaxation. In practice, even if the error in estimating relaxation is 100% of the value, the error in estimating exchange is only 1%, therefore more than acceptable. Far from coalescence, instead, you have to be cautious. The simplest thing to do is to verify that the T₂ changes monotonically with temperature.
In practice you collect 10 or more spectra at different temperatures. You also need the calibration curve of your probe (the instrument only reports the temperature around the probe; you need to know the temperature inside it, which can be measured spectroscopically, with a sample of methanol).
After extracting, by simulation, the rate of the exchange at each temperature, the plot of ln(k/T) versus 1/T gives a straight line; the enthalpy of activation can be derived from the slope and the entropy is derived from the intercept (Eyring equation). It's a mystery if these enthaply and entropy quantities remain the same at all temperatures or not. The linear plot should tell these things and will also tell if the whole work was correct or not.
If your software allows a computational least-square fit you can well try it, but I personally prefer the simple, old-style, manual fit. In theory there's no advantage in using a computational method, because the algorithm that finds the global minimum hasn't been invented yet. There is, however, something that a computer can do and we can't. It is the grand single fit of the whole experiment (the 10+ spectra) to find, via least squares, not the rates of exchange but directly the enthaply and entropy of activation. (They told me) the existence of this program has been mentioned in literature (years ago) but the program itself is not available.